SISTEMAS NUMERALES

Puede decirse que la historia de la computación comienza cuando el hombre adquiere la necesidad de contar. Seguramente en un principio el hombre comenzó a contar con los dedos, para después hacerlo mediante marcas en el piso o utilizando piedras. Con la invención de la escritura, diferentes civilizaciones encontraron sendas maneras de contar y más tarde, de efectuar operaciones. La figura 6 nos muestra, de una manera comparativa, algunos sistemas numerales.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figura 6. Esta figura nos muestra algunos sistemas numerales.

 

 

 

 

 

 

 

 

 

 

 

Figura 7. En la numeración maya un punto representa una unidad, una barra corresponde a cinco unidades, y el número cero es representado por una concha. Combinando estos signos pueden escribirse los números del 0 al 19. Para designar Números mayores al 19 se utiliza el sistema de posiciones: de abajo hacia arriba, la n-ésima posición representa unidades de n-ésimo orden.

Una de las escrituras más antiguas que se conoce es la egipcia. Esta civilización adoptó un sistema de contar de diez en diez, de manera que marcaban las unidades con líneas verticales y las decenas con un signo similar a la U invertida. Otras culturas adoptaron sistemas más complicados; por ejemplo, los babilonios contaban de 60 en 60, y aunque su sistema era muy poco práctico, se cree que de ellos provienen las bases del sistema actual de contar los minutos y los segundos.

Otra numeración antiguamente utilizada fue la romana, la cual era muy simple y permitía efectuar operaciones aritméticas aunque no con mucha sencillez. Aún perdura la tradición de utilizarla en algunos contextos específicos; por ejemplo, en las carátulas de los relojes, para denominar los tomos o capítulos de los libros, para escribir algunas fechas, etcétera.

Entre las culturas de América, es interesante señalar que los mayas contaron con un sistema numeral vigesimal muy avanzado y utilizaron el cero aun antes que en Europa o Asia. La figura 7 nos muestra esta numeración.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figura 8. En el sistema decimal se utiliza un criterio de posiciones con el cual cada dígito tiene un peso diferente, de acuerdo con una base diez. Esta figura nos muestra la forma en que se construye el número 1 968.

Podríamos continuar esta lista señalando más culturas y explicando sus sistemas de numeración, sin embargo, tan sólo queremos hacer hincapié en lo siguiente: la forma en que contamos actualmente, eso es, utilizando el sistema decimal (arábico), no es ni la única posible ni la única correcta, sino sólo una forma que hemos heredado de nuestros antepasados y que ha sobrevivido por ser simple y adecuada para nosotros debido a que tenemos diez dedos en las manos. Los principios de esta numeración se ilustran en la figura 8.

USO DE ARTEFACTOS PARA SUMAR

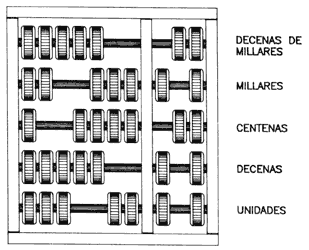
El siguiente paso en el desarrollo de la computación se dio con la invención de aparatos útiles para efectuar operaciones matemáticas. El ábaco es la primera calculadora o computadora de que tenemos noticias. Aunque se inventó hace aproximadamente 4 000 años, aún tiene un uso muy amplio en algunos países de Asia, debido a que se trata de una calculadora muy rápida y práctica, útil para efectuar operaciones de adición, substracción, multiplicación y división. Este artefacto se muestra en la figura 9.

Muchos años tuvieron que pasar antes de que se lograran progresos en el desarrollo de nuevas calculadoras. En 1617, el escocés John Napier inventa los llamados huesos de Napier o tablas de multiplicar (de donde proviene el nombre utilizado hasta nuestros días). Éstos consisten de una regla fija y otra móvil que se desliza sobre la primera, de manera que deja ver el producto de dos números cualesquiera (véase la figura 10). Posteriormente las tablas de Napier evolucionaron hasta llegar a la regla de cálculo, la cual funciona con el mismo principio pero es útil para llevar a cabo operaciones de multiplicación, división y raíz cuadrada, entre otras. Debido a su portabilidad, este artefacto tuvo una gran acogida en el mundo occidental y fue de uso frecuente hasta hace pocos años, cuando se generalizó el uso de las calculadoras de bolsillo.

A mediados del siglo XVII se inicia una nueva era de calculadoras mecánicas cuando, en 1642, Blaise Pascal, quien sólo contaba con 19 años de edad, introduce una máquina sumadora mecánica con el objeto de facilitar los cálculos de su padre (Figura 11). Esta máquina consistía en un sistema con ruedas pequeñas acopladas entre sí y que, de derecha a izquierda correspondían a unidades, decenas, centenas, etcétera. Estas ruedas se encontraban divididas en 10 partes iguales; de manera que para efectuar una suma se hacían girar manualmente un número de pasos acorde con el número que se deseaba introducir. La rotación completa de un círculo en la dirección positiva, causaba automáticamente que el círculo a su izquierda avanzara una posición. Para efectuar sustracciones el proceso era el inverso.

 

 

 

 

 

 

 

 

 

 

Figura 9. En el ábaco, cada barra horizontal contiene siete móviles separadas por una barra vertical. Aquéllas en el lado izquierdo valen uno, y las del lado derecho valen cinco; el número cero está representado cuando todas las cuentas están alejadas de la barra central. Las sumas se efectúan al mover, hacia la barra central, las cuentas correspondientes a la cantidad que se desea sumar.

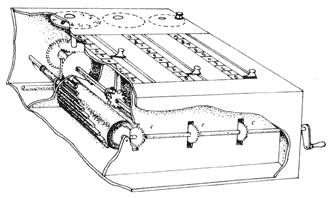
Algunos años más tarde, Leibniz inventa una máquina similar a la de Pascal pero más compleja, la cual podía sumar, restar, multiplicar y dividir. Es la computadora, ilustrada en la figura 12, se empleó extensivamente hasta el advenimiento de las computadoras electrónicas.

LA ERA DE LA PROGRAMACIÓN SE INICIA

Los siguientes avances significativos se logran hasta el siglo XIX, cuando Joseph Jacquard, quien era obrero en una fábrica de sedas de Lyon, introduce la idea de programar máquinas mediante el uso de tarjetas perforadas. La invención de Jacquard consistió en un telar que utilizaba tarjetas perforadas para controlar de manera automática el diseño y los colores de los tejidos. Esta idea es adaptada a la computación, en la llamada "máquina analítica" (Figura 13), por un matemático inglés llamado Charles Babbage, quien vivió obsesionado con el diseño y construcción de máquinas calculadoras. Más adelante hablaremos de esta máquina.

 

 

 

 

 

 

 

 

Figura 10. Esta figura muestra una variante de las "tablas de multiplicar", en la cual las tablas se ven substituidas por elementos que giran. Este aparato nunca llegó a funcionar satisfactoriamente.

 

 

 

 

 

 

 

Figura 11. Máquina de Pascal.

 

 

 

 

 

 

 

 

 

 

Figura 12.

 

 

Diagrama que muestra un corte de la máquina de calcular de Leibniz.

Babbage hizo su primer esbozo de una máquina calculadora a la que llamó máquina diferencial", en 1822. Sin embargo, constantemente tenía nuevas ideas que mejoraban el diseño original, por lo cual iba echando por tierra todo el trabajo realizado anteriormente. Es probable que esta situación hubiese continuado por muchos años, de no ser por una discusión que tuvo con su mecánico, después de la cual este último desmontó el taller y partió con todos los diseños. En esta coyuntura, Babbage tiene que empezar un nuevo diseño, y así concibe una calculadora totalmente nueva: su "máquina analítica", la cual habría de ser más fácil de construir y tendría mayor poder de cálculo que la anterior. Así, diseña una computadora mecánica digital a la cual habrían de suministrársele datos e instrucciones a seguir a través de tarjetas perforadas de acuerdo con un código. La computadora a su vez proporcionaría las soluciones también en forma de perforaciones en tarjeta. Como consecuencia, esta máquina "programable" ofrecía dos nuevas ventajas: i)por primera vez, una máquina sería capaz de utilizar durante un cálculo los resultados de otro anterior sin necesidad de reconfigurar la máquina, lo cual permitiría llevar a cabo cálculos iterativos, y ii) habría la posibilidad de que la computadora siguiese instrucciones alternas, dependiendo de los resultados de una etapa anterior del cálculo. Babbage describió esta máquina como "la máquina que se muerde la cola".

 

 

 

Figura 13. El dispositivo que se muestra en esta figura, forma parte de la máquina analítica de Babbage y nos da idea de su complicación; está diseñado para efectuar la operación de leamirba

multiplicar ( o dividir) un número por una potencia de diez.

Los planes de Babbage eran crear una máquina de no menos de 20 cifras de capacidad y precisión de seis cifras. Probablemente, las debilidades más grandes de este diseño fueron el cuidado y precisión requeridos para su construcción. De manera que, aunque su diseñador dedicó el resto de su vida, y gran parte de su fortuna, a tratar de terminar esta máquina, sólo pudo hacer una versión pequeña del modelo. De haberse construido, la máquina hubiese consistido de cerca de dos toneladas de maquinaria de relojería de latón y acero.

Para dar una idea al lector de la importancia de "la máquina que se muerde la cola", diremos que hasta ese momento, cada vez que se quería efectuar una serie de operaciones matemáticas, había que introducir, una a una y manualmente, todas las instrucciones y datos de la operación conforme se iban necesitando. A cada paso la máquina iba dando el resultado parcial de la operación específica efectuada, de manera que el "usuario" de la máquina podía decidir cuál sería la siguiente operación.